Intermediate component separation¶
[1]:
%load_ext autoreload
%autoreload 2
%matplotlib inline
[2]:
import numpy as np
import pylab
pylab.rcParams['figure.figsize'] = 12, 16
import healpy as hp
import pysm3
import pysm3.units as u
from fgbuster import get_instrument, get_sky, get_observation # Predefined instrumental and sky-creation configurations
from fgbuster.visualization import corner_norm
# Imports needed for component separation
from fgbuster import (CMB, Dust, Synchrotron, # sky-fitting model
basic_comp_sep) # separation routine
Input frequency maps¶
You have some frequency maps to clean, they can be either data or simulations.
Simple case¶
Let’s simulate a simple sky with pysm. ForeGroundBuster adds a couple of functions that make the process even easier.
[3]:
NSIDE = 64
sky_simple = get_sky(NSIDE, 'c1d0s0')
instrument = get_instrument('LiteBIRD')
freq_maps_simple = get_observation(instrument, sky_simple)
/Users/dpoletti/opt/miniconda3/envs/cosmo/lib/python3.7/site-packages/pysm3/utils/data.py:42: UserWarning: Retrieve data for pysm_2/camb_lenspotentialCls.dat (if not cached already)
warnings.warn(f"Retrieve data for {filename} (if not cached already)")
/Users/dpoletti/opt/miniconda3/envs/cosmo/lib/python3.7/site-packages/pysm3/utils/data.py:42: UserWarning: Retrieve data for pysm_2/delens_ells.txt (if not cached already)
warnings.warn(f"Retrieve data for {filename} (if not cached already)")
/Users/dpoletti/opt/miniconda3/envs/cosmo/lib/python3.7/site-packages/pysm3/utils/data.py:42: UserWarning: Retrieve data for pysm_2/dust_t_new.fits (if not cached already)
warnings.warn(f"Retrieve data for {filename} (if not cached already)")
/Users/dpoletti/opt/miniconda3/envs/cosmo/lib/python3.7/site-packages/pysm3/utils/data.py:42: UserWarning: Retrieve data for pysm_2/dust_q_new.fits (if not cached already)
warnings.warn(f"Retrieve data for {filename} (if not cached already)")
/Users/dpoletti/opt/miniconda3/envs/cosmo/lib/python3.7/site-packages/pysm3/utils/data.py:42: UserWarning: Retrieve data for pysm_2/dust_u_new.fits (if not cached already)
warnings.warn(f"Retrieve data for {filename} (if not cached already)")
/Users/dpoletti/opt/miniconda3/envs/cosmo/lib/python3.7/site-packages/pysm3/utils/data.py:42: UserWarning: Retrieve data for pysm_2/synch_t_new.fits (if not cached already)
warnings.warn(f"Retrieve data for {filename} (if not cached already)")
/Users/dpoletti/opt/miniconda3/envs/cosmo/lib/python3.7/site-packages/pysm3/utils/data.py:42: UserWarning: Retrieve data for pysm_2/synch_q_new.fits (if not cached already)
warnings.warn(f"Retrieve data for {filename} (if not cached already)")
/Users/dpoletti/opt/miniconda3/envs/cosmo/lib/python3.7/site-packages/pysm3/utils/data.py:42: UserWarning: Retrieve data for pysm_2/synch_u_new.fits (if not cached already)
warnings.warn(f"Retrieve data for {filename} (if not cached already)")
We will focus on polarization-only component separation
[4]:
freq_maps_simple = freq_maps_simple[:, 1:] # Select polarization
Spatially varying spectral indices¶
Let’s prepare also maps with spatially varying spectral indices. Similarly to the simple case above, we run the following (notice d1s1)
[5]:
NSIDE_PATCH = 8
sky_vary = get_sky(NSIDE, 'c1d1s1')
/Users/dpoletti/opt/miniconda3/envs/cosmo/lib/python3.7/site-packages/pysm3/utils/data.py:42: UserWarning: Retrieve data for pysm_2/camb_lenspotentialCls.dat (if not cached already)
warnings.warn(f"Retrieve data for {filename} (if not cached already)")
/Users/dpoletti/opt/miniconda3/envs/cosmo/lib/python3.7/site-packages/pysm3/utils/data.py:42: UserWarning: Retrieve data for pysm_2/delens_ells.txt (if not cached already)
warnings.warn(f"Retrieve data for {filename} (if not cached already)")
/Users/dpoletti/opt/miniconda3/envs/cosmo/lib/python3.7/site-packages/pysm3/utils/data.py:42: UserWarning: Retrieve data for pysm_2/dust_t_new.fits (if not cached already)
warnings.warn(f"Retrieve data for {filename} (if not cached already)")
/Users/dpoletti/opt/miniconda3/envs/cosmo/lib/python3.7/site-packages/pysm3/utils/data.py:42: UserWarning: Retrieve data for pysm_2/dust_q_new.fits (if not cached already)
warnings.warn(f"Retrieve data for {filename} (if not cached already)")
/Users/dpoletti/opt/miniconda3/envs/cosmo/lib/python3.7/site-packages/pysm3/utils/data.py:42: UserWarning: Retrieve data for pysm_2/dust_u_new.fits (if not cached already)
warnings.warn(f"Retrieve data for {filename} (if not cached already)")
/Users/dpoletti/opt/miniconda3/envs/cosmo/lib/python3.7/site-packages/pysm3/utils/data.py:42: UserWarning: Retrieve data for pysm_2/dust_beta.fits (if not cached already)
warnings.warn(f"Retrieve data for {filename} (if not cached already)")
/Users/dpoletti/opt/miniconda3/envs/cosmo/lib/python3.7/site-packages/pysm3/utils/data.py:42: UserWarning: Retrieve data for pysm_2/dust_temp.fits (if not cached already)
warnings.warn(f"Retrieve data for {filename} (if not cached already)")
/Users/dpoletti/opt/miniconda3/envs/cosmo/lib/python3.7/site-packages/pysm3/utils/data.py:42: UserWarning: Retrieve data for pysm_2/synch_t_new.fits (if not cached already)
warnings.warn(f"Retrieve data for {filename} (if not cached already)")
/Users/dpoletti/opt/miniconda3/envs/cosmo/lib/python3.7/site-packages/pysm3/utils/data.py:42: UserWarning: Retrieve data for pysm_2/synch_q_new.fits (if not cached already)
warnings.warn(f"Retrieve data for {filename} (if not cached already)")
/Users/dpoletti/opt/miniconda3/envs/cosmo/lib/python3.7/site-packages/pysm3/utils/data.py:42: UserWarning: Retrieve data for pysm_2/synch_u_new.fits (if not cached already)
warnings.warn(f"Retrieve data for {filename} (if not cached already)")
/Users/dpoletti/opt/miniconda3/envs/cosmo/lib/python3.7/site-packages/pysm3/utils/data.py:42: UserWarning: Retrieve data for pysm_2/synch_beta.fits (if not cached already)
warnings.warn(f"Retrieve data for {filename} (if not cached already)")
We can still modify the sky configuration. In this case, we change the nside over which the spectral indices are allowed to vary
[6]:
for spectral_param in [sky_vary.components[1].mbb_index,
sky_vary.components[1].mbb_temperature,
sky_vary.components[2].pl_index]:
spectral_param[:] = hp.ud_grade(hp.ud_grade(spectral_param.value, NSIDE_PATCH),
NSIDE) * spectral_param.unit
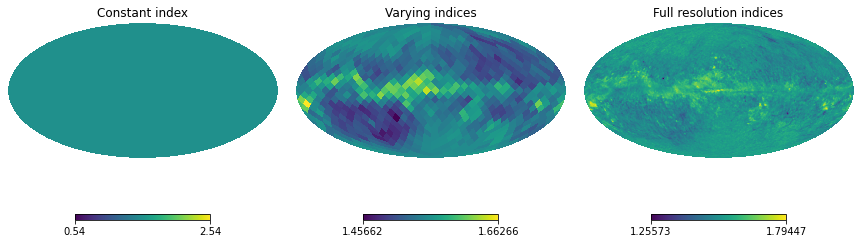
Here is how they look like in constant and varying case. The rightmost plot shows the full resolution pysm template.
[7]:
hp.mollview(sky_simple.components[1].mbb_index * np.ones(freq_maps_simple.shape[-1]),
sub=(1,3,1), title='Constant index')
hp.mollview(sky_vary.components[1].mbb_index, sub=(1,3,2), title='Varying indices')
hp.mollview(get_sky(NSIDE, 'c1d1s1').components[1].mbb_index, sub=(1,3,3), title='Full resolution indices')
And now we generate the maps and select polarization
[8]:
freq_maps_vary = get_observation(instrument, sky_vary)
freq_maps_vary = freq_maps_vary[:, 1:] # Select polarization
Component separation¶
The sky model we fit for is defined as a list of Component objects. They can be easily build from analytic SEDs, but for popular component types these are already implemented.
[9]:
components = [CMB(), Dust(353.), Synchrotron(23.)]
[10]:
# The starting point of the fit is the pysm default value, so let's shift it
components[1].defaults = [1.6, 22.]
components[2].defaults = [-2.7]
We are now ready to perform the component separation
[11]:
result = basic_comp_sep(components, instrument, freq_maps_simple,
options=dict(disp=True), # verbose output
)
Minimization started
Iter 1 x = [ 1.49898148 21.99773486 -2.70071941] First -logL = -23624280153.470936 N Eval = 3 Iter sec = 0.18 Cum sec = 0.18
Iter 2 x = [ 1.50038191 21.99280114 -3.06155996] Delta(-logL) = -34920.894505 N Eval = 6 Iter sec = 0.16 Cum sec = 0.34
Iter 3 x = [ 1.55864261 19.39583559 -3.10613116] Delta(-logL) = -32435.320213 N Eval = 8 Iter sec = 0.11 Cum sec = 0.45
Iter 4 x = [ 1.55361167 19.60436592 -3.08880451] Delta(-logL) = -451.340393 N Eval = 10 Iter sec = 0.11 Cum sec = 0.56
Iter 5 x = [ 1.55400653 19.58009044 -3.07347395] Delta(-logL) = -821.062992 N Eval = 11 Iter sec = 0.06 Cum sec = 0.61
Iter 6 x = [ 1.55482779 19.52493394 -3.0404649 ] Delta(-logL) = -1207.862453 N Eval = 12 Iter sec = 0.06 Cum sec = 0.67
Iter 7 x = [ 1.55461734 19.50932192 -3.01189623] Delta(-logL) = -373.809505 N Eval = 13 Iter sec = 0.06 Cum sec = 0.73
Iter 8 x = [ 1.55367034 19.53927742 -3.00856239] Delta(-logL) = -65.715275 N Eval = 14 Iter sec = 0.07 Cum sec = 0.80
Iter 9 x = [ 1.55176747 19.60109189 -3.00526796] Delta(-logL) = -123.544693 N Eval = 15 Iter sec = 0.06 Cum sec = 0.85
Iter 10 x = [ 1.5477383 19.73388696 -3.00117635] Delta(-logL) = -209.568089 N Eval = 16 Iter sec = 0.05 Cum sec = 0.91
Iter 11 x = [ 1.53909112 20.02377427 -2.9962294 ] Delta(-logL) = -150.647598 N Eval = 17 Iter sec = 0.07 Cum sec = 0.98
Iter 12 x = [ 1.54049588 19.98090185 -2.99889763] Delta(-logL) = -15.602619 N Eval = 18 Iter sec = 0.11 Cum sec = 1.08
Iter 13 x = [ 1.54016946 19.9936212 -2.99966614] Delta(-logL) = -1.515587 N Eval = 19 Iter sec = 0.08 Cum sec = 1.17
Iter 14 x = [ 1.54000003 20.00000132 -2.99998996] Delta(-logL) = -0.164299 N Eval = 20 Iter sec = 0.06 Cum sec = 1.23
Iter 15 x = [ 1.53999933 20.00002491 -2.99999723] Delta(-logL) = -0.000057 N Eval = 21 Iter sec = 0.06 Cum sec = 1.28
Iter 16 x = [ 1.53999983 20.00000621 -2.9999998 ] Delta(-logL) = 0.000000 N Eval = 22 Iter sec = 0.05 Cum sec = 1.34
Warning: Desired error not necessarily achieved due to precision loss.
Current function value: -23624350930.519215
Iterations: 16
Function evaluations: 23
Gradient evaluations: 22
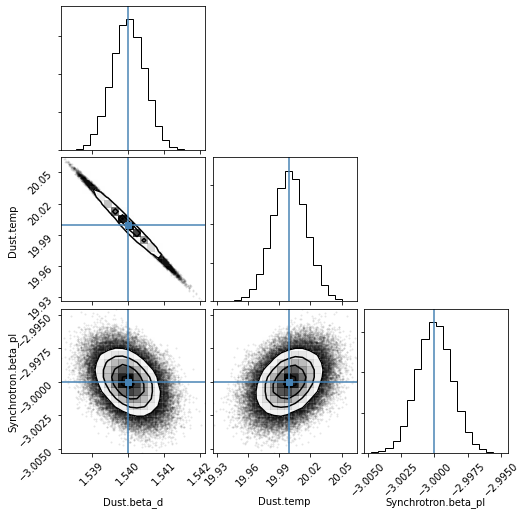
The input spectral parameters are recovered to numerical accuracy
[12]:
inputs = [sky_simple.components[1].mbb_index,
sky_simple.components[1].mbb_temperature.value,
sky_simple.components[2].pl_index]
print("%-20s\t%s\t%s" % ('', 'Estimated', 'Input'))
for param, val, ref in zip(result.params, result.x, inputs):
print("%-20s\t%f\t%f" % (param, val, ref))
Estimated Input
Dust.beta_d 1.540000 1.540000
Dust.temp 20.000006 20.000000
Synchrotron.beta_pl -3.000000 -3.000000
Their semi-analytic covariance is also provided, but remember that it is accurate only in the high signal-to-noise regime
[13]:
corner_norm(result.x, result.Sigma, labels=result.params, truths=inputs)
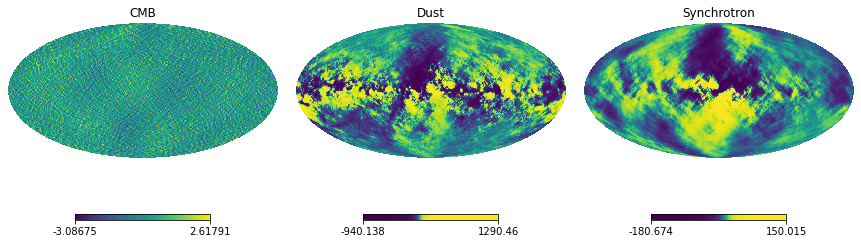
The amplitudes of the components are stacked in the s attribute and they are in the same format of the input frequency maps: Q and U healpix maps, in this case. Here is the U Stokes parameter for each of the components.
[14]:
hp.mollview(result.s[0,1], title='CMB', sub=(1,3,1))
hp.mollview(result.s[1,1], title='Dust', norm='hist', sub=(1,3,2))
hp.mollview(result.s[2,1], title='Synchrotron', norm='hist', sub=(1,3,3))
By taking the difference with the input template, we see that the error in the reconstruction is negligible.
[15]:
hp.mollview(result.s[1,1]
- sky_simple.components[1].U_ref.to(u.uK_CMB, equivalencies=u.cmb_equivalencies(sky_simple.components[1].freq_ref_P)).value,
title='Dust', norm='hist', sub=(1,2,1))
hp.mollview(result.s[2,1]
- sky_simple.components[2].U_ref.to(u.uK_CMB, equivalencies=u.cmb_equivalencies(sky_simple.components[2].freq_ref_P)).value,
title='Synchrotron', norm='hist', sub=(1,2,2))
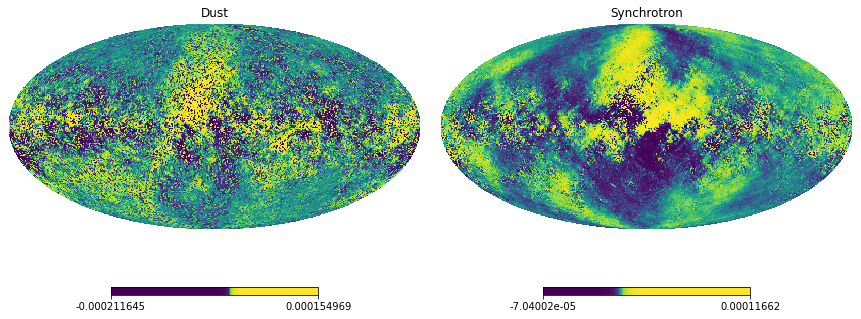
Component separation with varying indices¶
We now fit the spectral parameters independently over patches corresponding to healpix pixels with a given nside
[16]:
nside_fit = NSIDE_PATCH
result_vary = basic_comp_sep(components, instrument, freq_maps_vary, nside_fit)
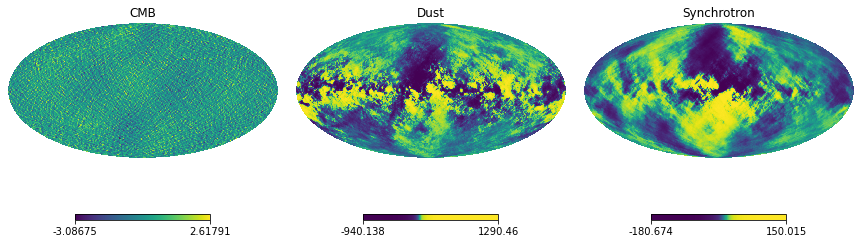
As in the previous case, the amplitudes of the components are stacked in the s.
[17]:
hp.mollview(result_vary.s[0,1], title='CMB', sub=(1,3,1))
hp.mollview(result_vary.s[1,1], title='Dust', norm='hist', sub=(1,3,2))
hp.mollview(result_vary.s[2,1], title='Synchrotron', norm='hist', sub=(1,3,3))
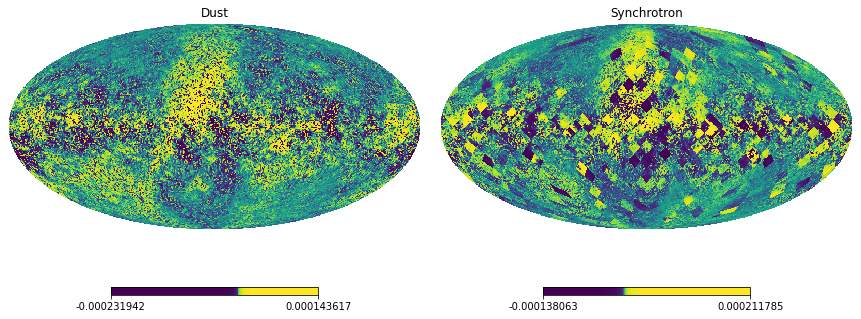
When we take the difference with the input templates, the residuals may be patchy. This is because the independent fit of the non-liner parameters has a different level of numerical accuracy for different patches. However, note that in all cases residuals are negligible: also this multi-patch cleaning has high accuracy.
[18]:
hp.mollview(result_vary.s[1,1]
- sky_vary.components[1].U_ref.to(u.uK_CMB, equivalencies=u.cmb_equivalencies(sky_vary.components[1].freq_ref_P)).value,
title='Dust', norm='hist', sub=(1,2,1))
hp.mollview(result_vary.s[2,1]
- sky_vary.components[2].U_ref.to(u.uK_CMB, equivalencies=u.cmb_equivalencies(sky_vary.components[2].freq_ref_P)).value,
title='Synchrotron', norm='hist', sub=(1,2,2))
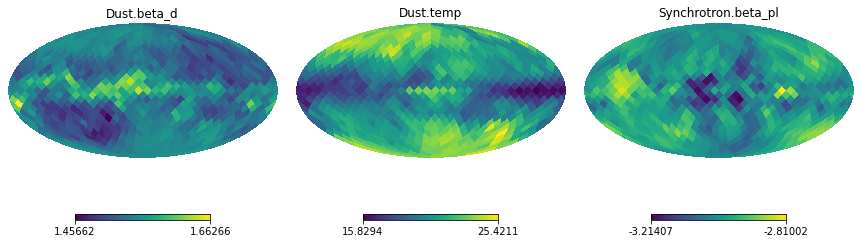
The same is true for the non-linear parameters. Here are their reconstructed maps.
[19]:
for i, par in enumerate(result.params):
hp.mollview(result_vary.x[i], title=par, sub=(1,3,i+1))
And here is the difference with the input templates.
[20]:
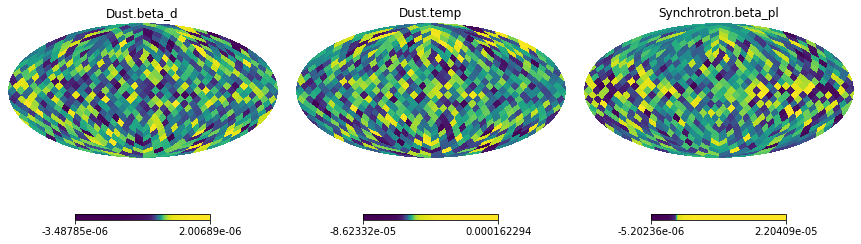
hp.mollview(hp.ud_grade(result_vary.x[0], NSIDE) -
sky_vary.components[1].mbb_index,
title=result.params[0], norm='hist', sub=(1,3,1))
hp.mollview(hp.ud_grade(result_vary.x[1], NSIDE) -
sky_vary.components[1].mbb_temperature.value,
title=result.params[1], norm='hist', sub=(1,3,2))
hp.mollview(hp.ud_grade(result_vary.x[2], NSIDE) -
sky_vary.components[2].pl_index,
title=result.params[2], norm='hist', sub=(1,3,3))